Paul Gader’s Ph.D. research, finished in 1986, was on parallel algorithms for Discrete Fourier Transforms and General Linear Transforms. He states, “The idea back then was that image processing could not be performed on general purpose CPUs. Therefore, researchers were investigating special image processing architectures. One was the so-called Massively Parallel Processor that would have a rectangular array of simple processors that could communicate only with their neighbors. There was a desire for automating the mapping of algorithms that required global computation to sequences of local calculations.”
Professor Gader investigated mathematical methods for doing that. He explains:
In the case of linear transformations, the problem could be a considered a matrix factorization problem. First consider the problem for a linear, or 1D, array of processors:

Figure 1. A linear array with 4 nodes. The neighbors of node \(x_1\) are nodes
\(x_1\) and \(x_2\), of node \(x_2\) are nodes \(x_1\), \(x_2\), \(x_3\), etc.
The neighbors of a node in the array are defined to be the node itself and the nodes immediately to the left and right of the node. At the ends, these are just the node on the left (at the right end) or the node on the right. Given a transformation, \(\mathbf{y} = \mathbf{Ax}\), where \(\mathbf{A}\) is a full \(M\times M\) matrix, the problem is to find a sequence of matrices \(\mathbf{A_1}, \mathbf{A_2}, \dots, \mathbf A_{M-1}\) such that each \(\mathbf A\) is tri-diagonal with \(\mathbf A = \mathbf{A_1}\mathbf{A_2}\ldots\mathbf A_{M-1}\). For any solution, \(\mathbf y = \mathbf A_1\mathbf A_2\ldots\mathbf A_{M-1}\mathbf x\).
For example, let
\(\mathbf A = \begin{bmatrix}0.67 &2.33 &0.00 &-0.33\\
1.00 &0.67 &2.00 &0.00\\
-1.33 &0.67 &0.67 &1.67\\
0.33 &-1.33 &0.33 &2.00
\end{bmatrix}\)
Then \(\mathbf A = \mathbf A_1\mathbf A_2\mathbf A_3\) where
\(\mathbf A_1 =\begin{bmatrix}
3 &-1 & 0 & 0\\
-1 & 3 &-1 & 0\\
0 &-1 & 3 &-1\\
0 & 0 &-1 & 3
\end{bmatrix}
\mathbf A_2 =
\begin{bmatrix}
0.33 &0.33 &0.00 &0.00\\
0.33 &0.33 &0.33 &0.00\\
0.00 &0.33 &0.33 &0.33\\
0.00 &0.00 &0.33 &0.33
\end{bmatrix}
\mathbf A_3 =
\begin{bmatrix}
2 & 1 & 0 & 0\\
-1 & 2 & 1 & 0\\
0 &-1 & 2 & 1\\
0 & 0 &-1 & 2
\end{bmatrix}\)
At each node in the linear array, the calculations \(\mathbf y_1 = \mathbf A_3\mathbf x\), \(\mathbf y_2 = \mathbf A\mathbf y_1\), and \(\mathbf y_3 = \mathbf A\mathbf y_2\) only require data only from their immediate neighbors in the array. Conceptually, a 2D array of processors leads to the same problem except the tri-diagonal matrix has to have a block format to account for neighbors in both the horizontal and vertical directions.
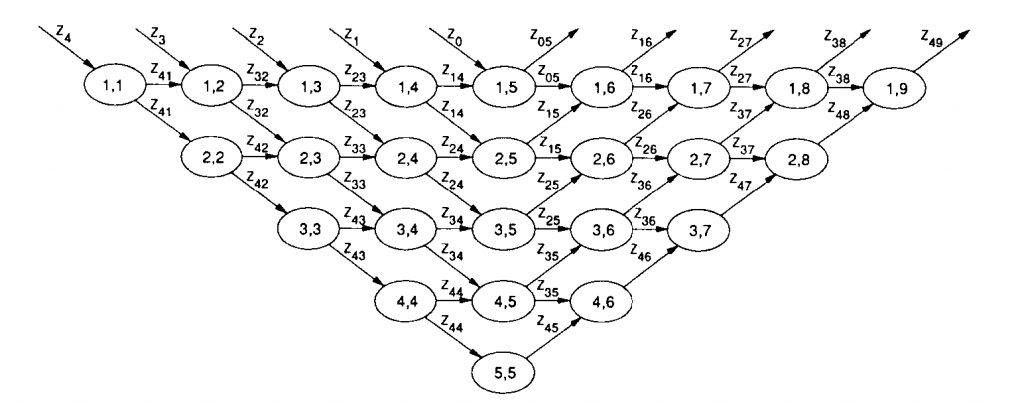
For example, one algorithm/architecture, referred to as a systolic algorithm/architecture, can process sequences of linear transforms, including Fourier transforms, at very high data rates. A sequence of signals, \(z_1\), …, \(z_t\), can be presented to the processor array. Once the array is filled, the Fourier transform of one signal is produced at each time step.
Want to know more? Click on these links:
Necessary and Sufficient Conditions for the Existence of Local Matrix Decompositions
Necessary and Sufficient Conditions for the Existence of Local Matrix Decompositions
In these papers, Paul Gader didn’t construct parallel algorithms but used group theory to help construct Superfast FFTs:
A Variant of the Gohberg-Semencul Formula Involving Circulant Matrices
Displacement Operator Based Decompositions of Matrices Using Circulants or Other Group Matrices
Professor Gader also worked on factorization of nonlinear transformations based on mathematical morphology as described in:
Local Decompositions of Gray-Scale Morphological Templates
Separable Decompositions and Approximations of Greyscale Mor-phological Templates
Keywords: Fast Fourier Transforms, Parallel Fast Fourier Transforms, Graphics Processing Units, GPUs, Matrix Factorization.